Topic: [Quiz] Answer the Bitcoin question and earn merits! #2 (Read 1053 times)
Edited out.
Mia Chloe is right. Mining is a Poisson process. One important characteristic of a Poisson process, is that it is memoryless; whether a block was found recently or not, does not give us a clue about the likelihood that another block will be found soon. Whether the last block was mined 2 hours ago or 10 minutes ago, the probability of mining a block within the next 10 minutes remains the same. (Of course, under the assumption that hashrate is constant and blocks are mined every 10 minutes on average)
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
Hahaha, I wasn't expecting to win against top members in the forum but I thought I was pretty close even though my presentation wasn't good enough. Thumbs up @Mia Chloe you deserve the win. @BlackHatcoiner hoping to participate again in your next contest. As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Code:
#include
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
if(y == 0 && x != 0) return 1;
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
if(y == 0 && x != 0) return 1;
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
Code:
For n=3, Λ=1, P=0.0613132
For n=4, Λ=1, P=0.01532830
For n=5, Λ=1, P=0.00306566
For n=6, Λ=1, P=0.000510944
For n=7, Λ=1, P=0.00000729
For n=4, Λ=1, P=0.01532830
For n=5, Λ=1, P=0.00306566
For n=6, Λ=1, P=0.000510944
For n=7, Λ=1, P=0.00000729
So in the end the exactly didn't matter and I guessed this was why after this:
Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block))
I still got the same 0.06133 which is roughly same as the 0.06131
But you're calculating exactly three in here. If P(block=3) = 1 - {every other possibility than P(block=3)), then you're calculating for exactly three. If you wanted to calculate for at least three, you would work out P(block >= 3), which is just 1 - P(block = 0) - P(block = 1) - P(block = 2) = 0.080302 ~= 8%.
I was actually working base on this Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block))
I still got the same 0.06133 which is roughly same as the 0.06131
But you're calculating exactly three in here. If P(block=3) = 1 - {every other possibility than P(block=3)), then you're calculating for exactly three. If you wanted to calculate for at least three, you would work out P(block >= 3), which is just 1 - P(block = 0) - P(block = 1) - P(block = 2) = 0.080302 ~= 8%.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
I wanted to check reality to see how often this occurred (start with Bitcoin block data available in CSV format, and download time.txt), but there is no accurate data on block times. In some cases the block time moves backwards.
That will be a little difficult. Block times are not accurate, as rightly said. Your best source of information is debug.log (in which it is written when your node received the blocks). But it won't be accurate either, because hashrate does not remain constant for a long time. So in the end the exactly didn't matter and I guessed this was why after this:
Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block))
I still got the same 0.06133 which is roughly same as the 0.06131
But you're calculating exactly three in here. If P(block=3) = 1 - {every other possibility than P(block=3)), then you're calculating for exactly three. If you wanted to calculate for at least three, you would work out P(block >= 3), which is just 1 - P(block = 0) - P(block = 1) - P(block = 2) = 0.080302 ~= 8%. Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block))
I still got the same 0.06133 which is roughly same as the 0.06131
Another fun fact. The probability of not finding any block for 10 minutes is the same as finding exactly one block; about 36.8%.
I wanted to check reality to see how often this occurred (start with Bitcoin block data available in CSV format, and download time.txt), but there is no accurate data on block times. In some cases the block time moves backwards.
That will be a little difficult. Block times are not accurate, as rightly said. Your best source of information is debug.log (in which it is written when your node received the blocks). But it won't be accurate either, because hashrate does not remain constant for a long time. 6.13%.
I wanted to check reality to see how often this occurred (start with Bitcoin block data available in CSV format, and download time.txt), but there is no accurate data on block times. In some cases the block time moves backwards. -snip-
So in the end the exactly didn't matter and I guessed this was why after this:Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block))
I still got the same 0.06133 which is roughly same as the 0.06131
My python code, works in similar way as your c++
I wrote mine as a code in python, to be Frank my code is not professional i`m still working on that
Poisson distribution was also spoken about on the bitcoin whitepaper in page 7 even in regards to your previous question
I did edit a part which was, math.factorial(3) to math.factorial(RandomNumber) Code:
import math
Parameter = 1
RandomNumber = 3
EulerNumber = 2.71828
Probability = (Parameter ** RandomNumber ) * (EulerNumber ** (-Parameter)) / math.factorial(RandomNumber)
RoundedProbability = round(Probability, 4)
Inpercentage = str(RoundedProbability * 100)
print ('The chance of having exactly three blocks mined within the next 10 minutes = ',
RoundedProbability, 'or', Inpercentage + '%')
Poisson distribution was also spoken about on the bitcoin whitepaper in page 7 even in regards to your previous question
Mia Chloe is right. Mining is a Poisson process. One important characteristic of a Poisson process, is that it is memoryless; whether a block was found recently or not, does not give us a clue about the likelihood that another block will be found soon. Whether the last block was mined 2 hours ago or 10 minutes ago, the probability of mining a block within the next 10 minutes remains the same. (Of course, under the assumption that hashrate is constant and blocks are mined every 10 minutes on average)
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Code:
#include
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
Code:
For n=3, Λ=1, P=0.0613132
For n=4, Λ=1, P=0.01532830
For n=5, Λ=1, P=0.00306566
For n=6, Λ=1, P=0.000510944
For n=7, Λ=1, P=0.00000729
The number of blocks expected to be found in a certain time follows the poisson distribution .
Which means the probability of finding exactly K block in T minutes is represented by the formula;
P(K,T)=(T/10)^K * e‐T/10/K!
Where; T=Time(mins) , K= Block
Inputting the values:
P(3,10) = (10/10)^3 * e‐(10/10)/3!
= 1³ * e‐¹/3!
= 0.0613.
For simplicity sake;
= 0.367879÷6
= 0.0613.
% = 6.13%
Mia Chloe is right. Mining is a Poisson process. One important characteristic of a Poisson process, is that it is memoryless; whether a block was found recently or not, does not give us a clue about the likelihood that another block will be found soon. Whether the last block was mined 2 hours ago or 10 minutes ago, the probability of mining a block within the next 10 minutes remains the same. (Of course, under the assumption that hashrate is constant and blocks are mined every 10 minutes on average)
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
I got the same answer on the below link?:As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Code:
#include
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
Code:
For n=3, Λ=1, P=0.0613132
For n=4, Λ=1, P=0.01532830
For n=5, Λ=1, P=0.00306566
For n=6, Λ=1, P=0.000510944
For n=7, Λ=1, P=0.00000729
https://bitcointalksearch.org/topic/m.63832047
For example, to find the chance of moving exactly three blocks in the next 10 minutes, we can use the Poisson distribution, which shows the fewest events in a given time.
Because of this, the chance of mining exactly three blocks in the next 10 minutes is about 0.06132, or 6.132%.
The C++ code that implements it is the following:
We get 0.0613132, or 6.13%.
Yes bro correct C++ is coming to me same.
Because of this, the chance of mining exactly three blocks in the next 10 minutes is about 0.06132, or 6.132%.
The C++ code that implements it is the following:
Code:
#include
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
Mia Chloe is right. Mining is a Poisson process. One important characteristic of a Poisson process, is that it is memoryless; whether a block was found recently or not, does not give us a clue about the likelihood that another block will be found soon. Whether the last block was mined 2 hours ago or 10 minutes ago, the probability of mining a block within the next 10 minutes remains the same. (Of course, under the assumption that hashrate is constant and blocks are mined every 10 minutes on average)
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
As displayed in Wikipedia, the formula is: P{N = n} = Λn * e-Λ / n!, where:
- n: the number of blocks to find within 10 minutes
- Λ: the number of blocks you would expect to find in 10 minutes.
For n=3, Λ=1, we get 0.0613132, or 6.13%.
The C++ code that implements it is the following:
Code:
#include
#include
using namespace std;
// constant number 'e'
const double Euler = std::exp(1.0);
// return x^y
int power(int x, int y){
if(y == 0 && x != 0) return 1;
int i, z = x;
for(i = 0; i < y; i++)
z *= z;
return z;
}
// factorial of integer x
int fact(int x){
if(x == 0) return 1;
int i, factorial = 1;
for(i = 1; i <= x; i++)
factorial *= i;
return factorial;
}
int main(){
// P{N = n} = Λ^n * e^-Λ / n!
// n: number of blocks to find within given time frame
// Λ or lambda: number of blocks you would expect to find in 10 minutes
int n = 3, lambda = 1;
double P = power(lambda, n) * pow(Euler, -lambda) / fact(n);
cout << P << endl;
}
Just compile with "g++ -o mining mining.cpp" and run with "./mining".
See how abruptly improbable it becomes as you increase n.
Code:
For n=3, Λ=1, P=0.0613132
For n=4, Λ=1, P=0.01532830
For n=5, Λ=1, P=0.00306566
For n=6, Λ=1, P=0.000510944
For n=7, Λ=1, P=0.00000729
Short introduction for anyone who missed the first quiz:
I decided to start these forum quiz-series, where I'll be asking questions of educational character, to improve the average user's knowledge around Bitcoin. The questions will mostly be technical and historical. To create an incentive, I will generously merit the first person who replies with the correct answer. If that is not good enough incentive, I'll create a leaderboard!
- Your answer needs to be explanatory. Not just a yes-no or a single number.
- If nobody finds the answer until the cut-off date, I will submit it.
- Have fun! It's a game.
The first question was a tribute to the whitepaper. Now let's see how good we are at math.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Cut-off date: 27/03/2024.
Unfortunately, we can't calculate the exact chance of having exactly three blocks mined within the next 10 minutes with the given information. Here's why:
Block mining is not deterministic: While the average block time might be 10 minutes, it's not guaranteed. The actual time between blocks can vary due to factors like mining difficulty.
Poisson distribution, not binomial: Since new blocks are independent events (one block doesn't affect the next), a Poisson distribution would be more appropriate for this scenario. This model considers the average rate of events (blocks mined) within a specific timeframe (10 minutes).
However, we can explore the likelihood of having around three blocks mined in 10 minutes using the Poisson distribution.
Here's what we'd need:
Average block time: We're given that it's 10 minutes on average.
With this information, we can calculate the lambda (λ) parameter for the Poisson distribution, which represents the average number of events (blocks mined) expected in a given timeframe (10 minutes).
λ = average rate (blocks/minute) * time (minutes)
λ = 1 block / 10 minutes * 10 minutes
λ = 1
Using a Poisson probability calculator or statistical software, we can then estimate the probability of getting exactly 3 blocks (k = 3) within 10 minutes (λ = 1)
This will give you a probability value, but it won't be an exact chance due to the inherent randomness of block mining times.
Giving this a try :
1.566E-14
1.566E-14
Using this formula I got 0
Where :
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 10
e = 2.71828
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 1/10 =0.1
e = 2.71828
Probability of 3 blocks mined in an average of 10 minutes = 0.06132
My interpretation is if the exactly is :
With in the 10 minutes time interval
0 to infinite block can be mined while though my constrict is 3 block
Then
Pr (3 block) = 1 - (Pr( ≤2 block) + Pr (>3 block)
Where :
Pr( ≤2 block) = Pr (0 block) + Pr (1 block) + Pr (2 block)
Pr (>3 block) = Pr (4 block) + Pr (5 block) + Pr (6 block)...
Though this tends to infinity but I stop in block 6 since I'm using 5 decimal place
But my final answer was Pr(3 block) = 0.06133 which is the similar to the Probability of 3 blocks mined in an average of 10 minutes = 0.06132
its worth noting.. someone done a study in ~2018 of the first 535k blocks
this is what they said
so dont use a blocks time stamp of blockchain history to gauge how often 3 blocks were solved in under 10 minutes.. timestamps are not accurate measure of actual time they were actually solved
this is what they said
Quote
For "shortest", since timestamps are not strictly enforced and can be fudged accidentally or intentionally, it is possible for a block to have an earlier timestamp than its predecessor, by up to 2 hours (7200 seconds), in which case the time difference is negative. This has happened 13828 times. The most negative difference is −7125 seconds (1 hour 58 minutes 45 seconds) between blocks 156113 and 156114.
so dont use a blocks time stamp of blockchain history to gauge how often 3 blocks were solved in under 10 minutes.. timestamps are not accurate measure of actual time they were actually solved
Sir, the probability of having exactly 3 blocks mined within the next 10 minutes is approximately 0.0613, or 6.13%.
I'm learning alot here, but i believe this answer of yours is AI generated. If you did it yourself then show working, or at least explain how you got the answer.
Here is one of the rules of the quiz, your answer must be explanatory.
- Your answer needs to be explanatory. Not just a yes-no or a single number.
It seems newbies aren't allowed to send a picture here because I did my calculations in my notebook as it would have been easier for me to drop a picture of my calculations. I may be wrong though with my answer but am delighted to participate.
I would be glad to see your calculations! Drop them in talkimg and post them as a link (since you're prohibited to posting images). 
here is my calculation, i hope you can see it clearly. 
I tried computing the blocks mined within 10minutes which also includes that of 10 minutes and less meaning lambda would vary by a common difference of 0.1 by using 9,8,7...... Minutes.
More details in my solution above
A miner with the advantage of 51% attack will be able to
1.double send coins and also
2. prevent confirmation of transactions,
but to his disadvantage he won't be able to
1. Reverse confirmed transactions
2.creat new coins
If someone has the majority control of hashing power then he can decide which transactions to include in the next block.
1.double send coins and also
2. prevent confirmation of transactions,
but to his disadvantage he won't be able to
1. Reverse confirmed transactions
2.creat new coins
If someone has the majority control of hashing power then he can decide which transactions to include in the next block.
It can be 0... That's a fact.
I just gave two recent examples. How can it have zero probability?Sorry, it was a typo, I want to say "can't".
I have seen both scenarios in the past, the one that shows us 1 block in 1 hour, and the one that shows us 5 blocks in 10 minutes... And the first scenario feels terrible, waiting more than 1 hour for a confirmation is a nightmare.
Getting back to the main question, what's the probability? i would say 33%, because having 1 block in 10 minutes has a chance of 100%, having 2 is 50%, and 3 33%... But my logic is too basic, as i mentioned in the past post, a lot of facts are involved.
The probability of mining a new block every 10 minutes is about 1/10 or 10% on average.
This is incorrect, and thus, so is everything that follows. Binomial probability is not the method to compute it either. It seems newbies aren't allowed to send a picture here because I did my calculations in my notebook as it would have been easier for me to drop a picture of my calculations. I may be wrong though with my answer but am delighted to participate.
I would be glad to see your calculations! Drop them in talkimg and post them as a link (since you're prohibited to posting images). The chance of having exactly three blocks mined in 10 minutes is 0.001
It is not. You can verify by checking the blockchain. 0.001 is 0.1%, which means that three blocks in 10 minutes would have to be mined only once in 1000 times. By checking the three most recent blocks (835552, 835553 and 835554), I can see that they were all mined within 10 minutes. If you go a little past that, blocks 835541, 835540, 835539 and 835538 were all mined within 10 minutes! I'm sure you will find more such cases, a lot more frequently than once in 1000.Using this formula I got 0
It can be 0... That's a fact.
I just gave two recent examples. How can it have zero probability? Using this formula I got 0
Where :
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 10
e = 2.71828
It can't be 0... That's a fact.
It's a tricky question because there are factors involved like Mining difficulty and the total hashing power on the network... The 10 minutes is a constant written on the Bitcoin code, but the ones who find the block are the miners, so, if the difficulty is high and the hashing power is low, the probability of finding 3 blocks in 10 minutes is lower than the case where the hashing power is high.
actually this is a good question.
as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
I actually thought about this but I didn't make use of values ≥3 because the question asked was for exactly 3 blocks.as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
If not I would simply calculate that for 2 blocks and 1 block and then subtract the value from 1 to get that for the number of possible mined blocks geater than of equal to 3 since;
Pr(<2 blocks) + Pr(≥3 blocks) = 1
So Pr(≥3 blocks) = 1- Pr(<2 blocks)
Since Pr(≥3 blocks) more like tends to infinity and thus would be more difficult to compute as you would have to solve for the probability of 3,4 ,5,6,7........ Till infinity the more Pr(≥3 blocks) outcomes you compute, the more accurate your probability.
yeah but pretend the network rips 3 blocks in the first 3 seconds. the next 9+ minutes could kill it off.
So I would think you need poisson for
4+5+6+7+8+9+10 is pretend 1.4%
take that 6.13-1.4 = 4.73 and know you are close.
If you disregard the chance of the over block events you you be wrong.
basically because he wants exactly 3 not 4 or 5 or 6 or any higher ones.
Not doing the math for
4
5
6
7
8
9
...
20 but each one is less by a fairly large factor
Using this formula I got 0
Where :
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 10
e = 2.71828
Sir, the probability of having exactly 3 blocks mined within the next 10 minutes is approximately 0.0613, or 6.13%.
actually this is a good question.
as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
I actually thought about this but I didn't make use of values ≥3 because the question asked was for exactly 3 blocks.as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
If not I would simply calculate that for 2 blocks and 1 block and then subtract the value from 1 to get that for the number of possible mined blocks geater than of equal to 3 since;
Pr(<2 blocks) + Pr(≥3 blocks) = 1
So Pr(≥3 blocks) = 1- Pr(<2 blocks)
Since Pr(≥3 blocks) more like tends to infinity and thus would be more difficult to compute as you would have to solve for the probability of 3,4 ,5,6,7........ Till infinity the more Pr(≥3 blocks) outcomes you compute, the more accurate your probability.
Or 0.1%, ie 1/1000. So the probability of mining three blocks in the next 10 minutes is about 0.1% or 1/1000
To find the probability of having exactly three blocks mined, I multiplied the probability of a single block being mined three times, that is, 1/10 * 1/10 * 1/10 = 1/1000
The chance of having exactly three blocks mined in 10 minutes is 0.001
actually this is a good question.
as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
if you did if for
4 blocks you would get a smaller number. say 1 percent
5 blocks you would get a smaller number than 1 percent say .1 percent
you could do that for
4,5,6,7,8,9,10 and maybe that gives a close enough estimate for more than 3 blocks maybe it is 1.4%
then take the 6.13-1.4 and get 4.73%
not perfect but if you extend to 20 blocks in 10 minutes it would be very accurate.
So I say
Poisson distribution for 3 blocks = 6.13
then add poisson for
4
5
6
7
8
9
10 subtract from poisson for 3 and very accurate
more accurate
poisson
for
11
12
13
14
15
16
17
18
19
20 add to 4-10 and subtract that from poisson for 3
since the possibility is endless but unlikely I would accept
poisson for 3 - poisson's for (4+5+6+7+8+9+10) as close enough
as the 6.13 percent answer left out all the chances above 3 blocks.
so it is close but no cigar.
if you did if for
4 blocks you would get a smaller number. say 1 percent
5 blocks you would get a smaller number than 1 percent say .1 percent
you could do that for
4,5,6,7,8,9,10 and maybe that gives a close enough estimate for more than 3 blocks maybe it is 1.4%
then take the 6.13-1.4 and get 4.73%
not perfect but if you extend to 20 blocks in 10 minutes it would be very accurate.
So I say
Poisson distribution for 3 blocks = 6.13
then add poisson for
4
5
6
7
8
9
10 subtract from poisson for 3 and very accurate
more accurate
poisson
for
11
12
13
14
15
16
17
18
19
20 add to 4-10 and subtract that from poisson for 3
since the possibility is endless but unlikely I would accept
poisson for 3 - poisson's for (4+5+6+7+8+9+10) as close enough
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
So I'd say that there's a 6.13% chance of having exactly three blocks mined within the next 10 minutes.
I could have loved to explain how I got my answer in details but my keyboard isn't giving me every thing I need to type.
The poisson formula looks like this, p(x;a) = (e^(-a) *a^x) / x!
I used "a" to replace the symbol I couldn't find in my keyboard.
It seems newbies aren't allowed to send a picture here because I did my calculations in my notebook as it would have been easier for me to drop a picture of my calculations. I may be wrong though with my answer but am delighted to participate.
The probability of mining a new block every 10 minutes is about 1/10 or 10% on average.
If each block has a 10% chance of being mined, then the probability of mining three blocks is:
(10% * 10% * 10%) = 0.1 * 0.1 * 0.1 = 0.001
Or 0.1%, ie 1/1000. So the probability of mining three blocks in the next 10 minutes is about 0.1% or 1/1000.
Otherwise,,,
Since there is a binomial probability for each event (yes or no), the probability will be the average position of the numbers.
Given its value, the binomial probability for each event will be 1/2.
Then the probabilities for the first three events would be:
(1/2) * (1/2) * (1/2) = 1/8
If each block has a 10% chance of being mined, then the probability of mining three blocks is:
(10% * 10% * 10%) = 0.1 * 0.1 * 0.1 = 0.001
Or 0.1%, ie 1/1000. So the probability of mining three blocks in the next 10 minutes is about 0.1% or 1/1000.
Otherwise,,,
Since there is a binomial probability for each event (yes or no), the probability will be the average position of the numbers.
Given its value, the binomial probability for each event will be 1/2.
Then the probabilities for the first three events would be:
(1/2) * (1/2) * (1/2) = 1/8
If 3 blocks was mined 10 minutes, that means each transaction would be mined within 1/10^3 and 0.0027 per transaction.
1/10^3 gotten from the λ and the 0.0027 is 1/10^3
These are some non-understandable math. Why 10^3, how did you work out 0.0027 and what does it mean?1/10^3 gotten from the λ and the 0.0027 is 1/10^3
We know the formula of probability is :- possibility= (Number of favorable outcomes of events / Number of possible outcomes)
That's not the correct formula to use. Your formula makes sense in finite sets. For example, the odds of getting an even number from a dice roll. Code:
{Total of even integers from 1 to 6} / {Total integers from 1 to 6} = 3 / 6 = 0.5
The set of all possible outcomes in the Bitcoin network within 10 minutes is infinite.
Before I unveil the answer, I want to leave the thread for a few hours. Maybe someone wants to correct the replies above.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Since Probability simply means the extent to which an event likely to occur, and we all know that it takes approximately 10 minutes for each block to be mined, I think the answer to this is what I will be giving in the calculation down below.
FORMULA FOR PROBABILITY
P(A) = Number of times A occur / Total number of possible outcomes
Where;
Number of times A occur = 10
Total number of possible outcomes = 3
Probability = ?
P(A) = (10 / 3) = 3.33
I wrote mine as a code in python, to be Frank my code is not professional i`m still working on that
Poisson distribution was also spoken about on the bitcoin whitepaper in page 7 even in regards to your previous question
Code:
import math
Parameter = 1
RandomNumber = 3
EulerNumber = 2.71828
Probability = (Parameter ** RandomNumber ) * (EulerNumber ** (-Parameter)) / math.factorial(RandomNumber)
RoundedProbability = round(Probability, 4)
Inpercentage = str(RoundedProbability * 100)
print ('The chance of having exactly three blocks mined within the next 10 minutes = ',
RoundedProbability, 'or', Inpercentage + '%')
Parameter = 1
RandomNumber = 3
EulerNumber = 2.71828
Probability = (Parameter ** RandomNumber ) * (EulerNumber ** (-Parameter)) / math.factorial(RandomNumber)
RoundedProbability = round(Probability, 4)
Inpercentage = str(RoundedProbability * 100)
print ('The chance of having exactly three blocks mined within the next 10 minutes = ',
RoundedProbability, 'or', Inpercentage + '%')
Poisson distribution was also spoken about on the bitcoin whitepaper in page 7 even in regards to your previous question
I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.
But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.
But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.
Thanks for the heads up
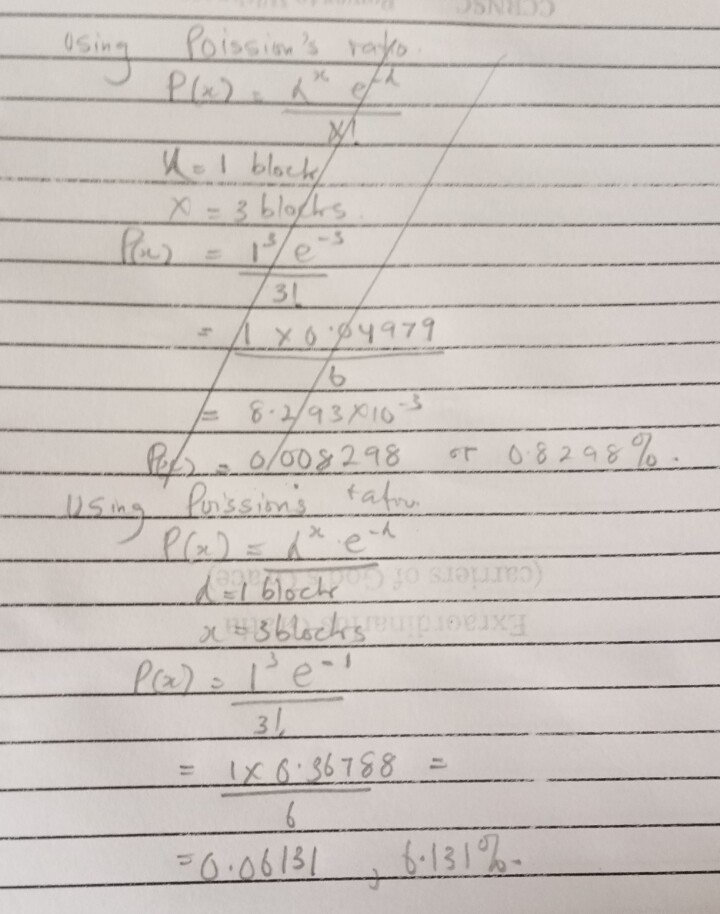
I mistakenly substituted 3 instead of 1
I also got the same result using this formula. However, the word “exactly” in the BlackHatCoiner`s assignment confuses me. After all, this implies that exactly 3 blocks and no more should be mined in 10 minutes, and that the situation where 3 were mined and the fourth was already started to be mined is not suitable, as far as I understand. That is, after exactly ten minutes, exactly three blocks should be mined, and the extraction of the fourth should fall on the eleventh minute. And if my thoughts are correct, then Poison Distribution formula does not take this into account and the probability is calculated incorrectly, because it is greater than it actually is.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Cut-off date: 27/03/2024.
I'm using mathematics to explain the question:
probability 1/10 ...K= P(3:1) that (3 blocks per minute) = (e^-1-1^3)/3! =1/e.6 = 0.0613 ~ 6.13
^ is a power function
mean ^-1 ...-1 is to the function "e" same as ^3 to the function "1"
The first question was a tribute to the whitepaper. Now let's see how good we are at math.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Cut-off date: 27/03/2024.
Not like I have a choice but I preferred the first question better
These are very critical mining questions with a mix of math.
I am terrible at math.
I will return to this thread after the cut-off date - 27/03/2024 and try just study the answer of whoever gets the quiz correctly. Just maybe in the future I will be able to participate.
Poison Distribution explains it all
If the hashrate is not constant and we experience a memoryless event through the poison process, which describe the number of blocks that can be possily mined at a particular given time interval, Poinson distribution explains how such an event could occur on a multiple times, you can learn more from these https://careerfoundry.com/en/blog/data-analytics/what-is-poisson-distribution/
If the hashrate is not constant and we experience a memoryless event through the poison process, which describe the number of blocks that can be possily mined at a particular given time interval, Poinson distribution explains how such an event could occur on a multiple times, you can learn more from these https://careerfoundry.com/en/blog/data-analytics/what-is-poisson-distribution/
I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.
But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.
But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.
Thanks for the heads up
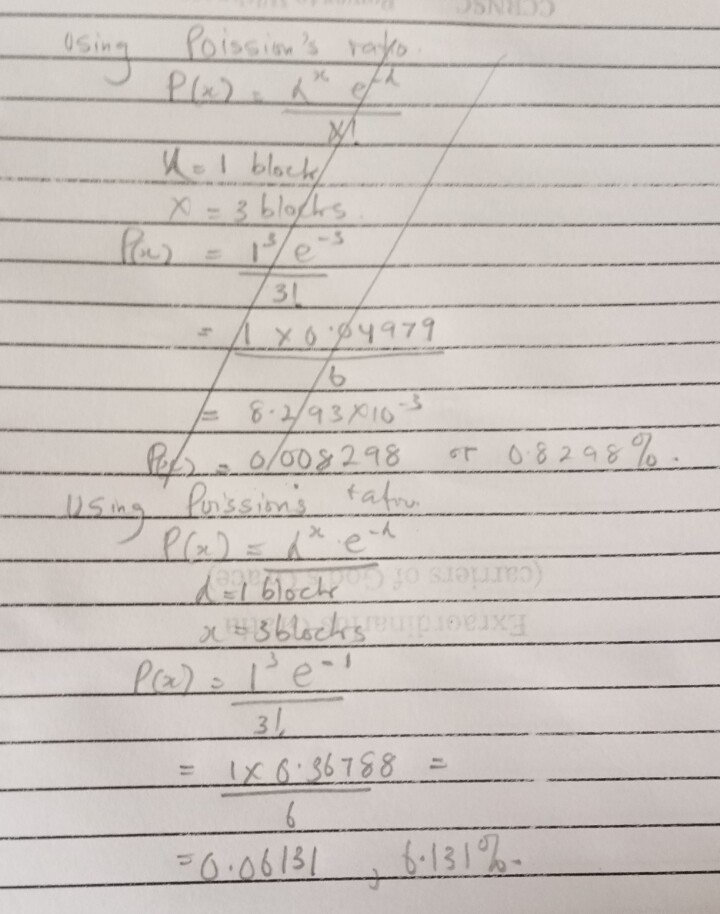
I mistakenly substituted 3 instead of 1
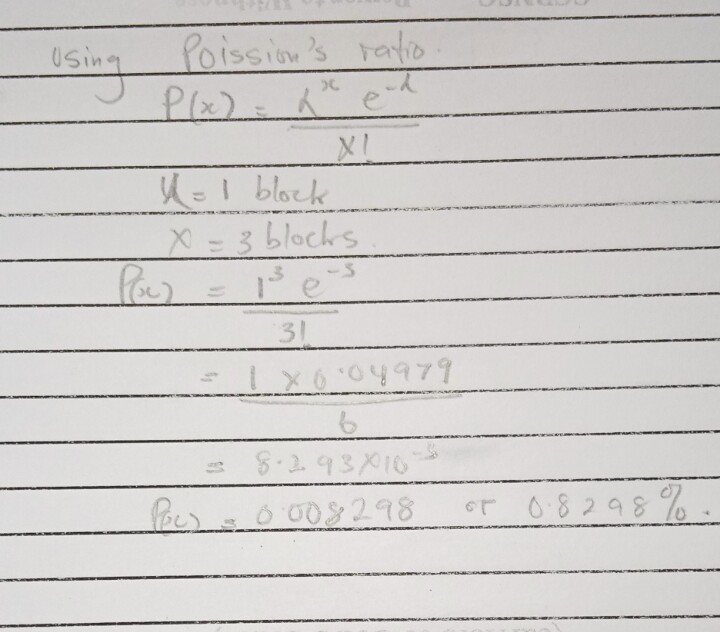
Here is my final solution
The time was same in both cases so time is constant.
0.008298
I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.
But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.
I am explaining your question mathematically,
We know the formula of probability is :- possibility= (Number of favorable outcomes of events / Number of possible outcomes)
suppose :- Number of favorable outcomes of events {P} and Number of possible outcomes {X}
As this as this:- Number of favorable outcomes of events(P):- 10
Number of possible outcomes(X):- 3
Therefore :- possibility= (P/X)
= (10/3)
=30%
With a 30% chance, since a new block is mined every 10 minutes, it is possible to mine about 3 blocks every 10 minutes. And in 10 minutes the chance of having exactly three blocks mined is 30% or (10/3)%.
We know the formula of probability is :- possibility= (Number of favorable outcomes of events / Number of possible outcomes)
suppose :- Number of favorable outcomes of events {P} and Number of possible outcomes {X}
As this as this:- Number of favorable outcomes of events(P):- 10
Number of possible outcomes(X):- 3
Therefore :- possibility= (P/X)
= (10/3)
=30%
With a 30% chance, since a new block is mined every 10 minutes, it is possible to mine about 3 blocks every 10 minutes. And in 10 minutes the chance of having exactly three blocks mined is 30% or (10/3)%.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Hmm. Am not a good mathematics student but I would like to try my best on this.If 3 blocks was mined 10 minutes, that means each transaction would be mined within 1/10^3 and 0.0027 per transaction.
1/10^3 gotten from the λ and the 0.0027 is 1/10^3
P=1/3
P=0.33
Or 33.33%
Sometimes, for more than 10 minutes, no block is found. So, the probability of finding one block within the next 10 minutes is not 100%. P=0.33
Or 33.33%
P=1/3
P=0.33
Or 33.33%
Sometimes, for more than 10 minutes, no block is found. So, the probability of finding one block within the next 10 minutes is not 100%. P=0.33
Or 33.33%
Since a block is mined every 10 minutes the probability of mining 3 blocks in 10 minutes will be
Number of possible blocks -->1
Number of required block --> 3
Keeping time constant (10minutes)
P=1/3
P=0.33
Or 33.33%
Number of possible blocks -->1
Number of required block --> 3
Keeping time constant (10minutes)
P=1/3
P=0.33
Or 33.33%
Short introduction for anyone who missed the first quiz:
I decided to start these forum quiz-series, where I'll be asking questions of educational character, to improve the average user's knowledge around Bitcoin. The questions will mostly be technical and historical. To create an incentive, I will generously merit the first person who replies with the correct answer. If that is not good enough incentive, I'll create a leaderboard!
- Your answer needs to be explanatory. Not just a yes-no or a single number.
- If nobody finds the answer until the cut-off date, I will submit it.
- Have fun! It's a game.
The first question was a tribute to the whitepaper. Now let's see how good we are at math.
Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.
Cut-off date: 27/03/2024.
Jump to: