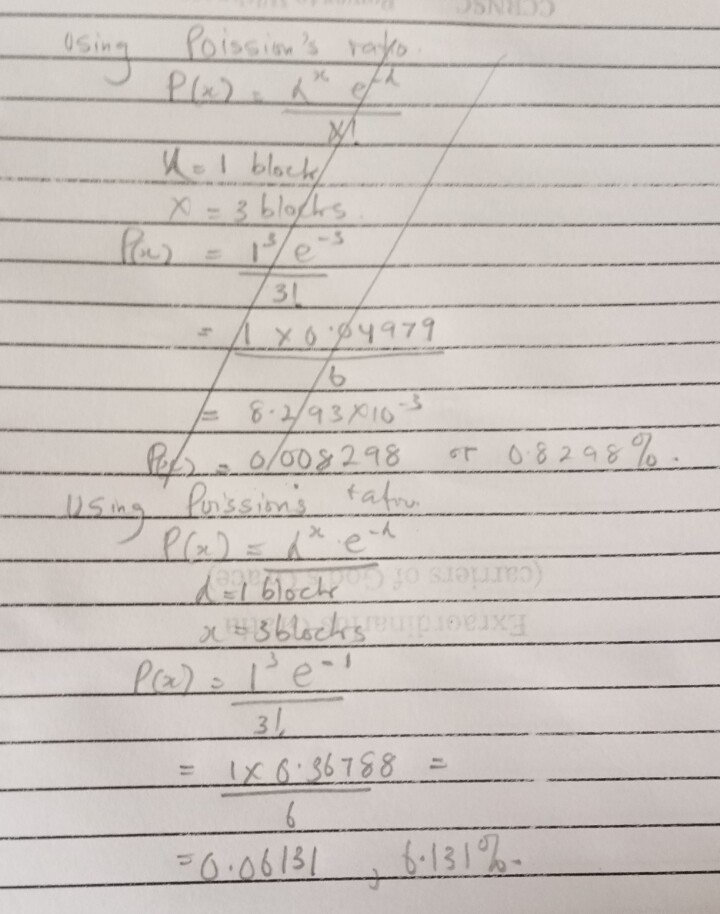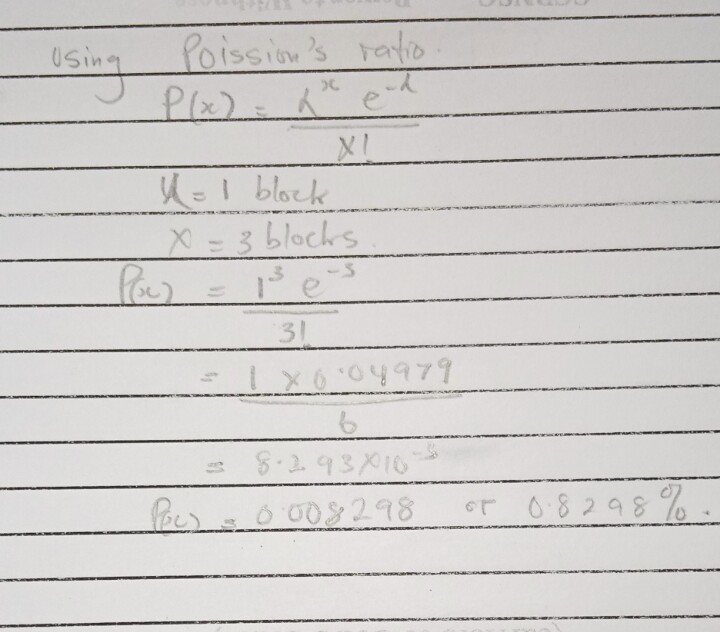[Quiz] Answer the Bitcoin question and earn merits! #2 - page 2.

seoincorporation

legendary

Activity: 3346

Merit: 3125

Quote from: BlackHatCoiner on March 20, 2024, 12:13:37 PM

Quote from: seoincorporation on March 20, 2024, 11:58:33 AM

It can be 0... That's a fact.

I just gave two recent examples. How can it have zero probability?

Sorry, it was a typo, I want to say "can't".

I have seen both scenarios in the past, the one that shows us 1 block in 1 hour, and the one that shows us 5 blocks in 10 minutes... And the first scenario feels terrible, waiting more than 1 hour for a confirmation is a nightmare.

Getting back to the main question, what's the probability? i would say 33%, because having 1 block in 10 minutes has a chance of 100%, having 2 is 50%, and 3 33%... But my logic is too basic, as i mentioned in the past post, a lot of facts are involved.

BlackHatCoiner

legendary

Activity: 1512

Merit: 7340

Farewell, Leo

Quote from: Ricardo11 on March 20, 2024, 09:43:40 AM

The probability of mining a new block every 10 minutes is about 1/10 or 10% on average.

This is incorrect, and thus, so is everything that follows. Binomial probability is not the method to compute it either.

Quote from: AmaGold70 on March 20, 2024, 09:54:45 AM

It seems newbies aren't allowed to send a picture here because I did my calculations in my notebook as it would have been easier for me to drop a picture of my calculations. I may be wrong though with my answer but am delighted to participate.

I would be glad to see your calculations! Drop them in talkimg and post them as a link (since you're prohibited to posting images).

Quote from: Cityhunter34 on March 20, 2024, 10:10:07 AM

The chance of having exactly three blocks mined in 10 minutes is 0.001

It is not. You can verify by checking the blockchain. 0.001 is 0.1%, which means that three blocks in 10 minutes would have to be mined only once in 1000 times. By checking the three most recent blocks (835552, 835553 and 835554), I can see that they were all mined within 10 minutes. If you go a little past that, blocks 835541, 835540, 835539 and 835538 were all mined within 10 minutes! I'm sure you will find more such cases, a lot more frequently than once in 1000.

Quote from: Amphenomenon on March 20, 2024, 11:44:04 AM

Using this formula I got 0

Quote from: seoincorporation on March 20, 2024, 11:58:33 AM

It can be 0... That's a fact.

I just gave two recent examples. How can it have zero probability?

seoincorporation

legendary

Activity: 3346

Merit: 3125

Quote from: Amphenomenon on March 20, 2024, 11:44:04 AM

Using this formula I got 0
Where :
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 10
e = 2.71828

It can't be 0... That's a fact.

It's a tricky question because there are factors involved like Mining difficulty and the total hashing power on the network... The 10 minutes is a constant written on the Bitcoin code, but the ones who find the block are the miners, so, if the difficulty is high and the hashing power is low, the probability of finding 3 blocks in 10 minutes is lower than the case where the hashing power is high.

philipma1957

legendary

Activity: 4256

Merit: 8551

'The right to privacy matters'

Quote from: Mia Chloe on March 20, 2024, 10:37:35 AM

Quote from: philipma1957 on March 20, 2024, 10:02:04 AM

actually this is a good question.

as the 6.13 percent answer left out all the chances above 3 blocks.

so it is close but no cigar.

I actually thought about this but I didn't make use of values ≥3 because the question asked was for exactly 3 blocks.

If not I would simply calculate that for 2 blocks and 1 block and then subtract the value from 1 to get that for the number of possible mined blocks geater than of equal to 3 since;
Pr(<2 blocks) + Pr(≥3 blocks) = 1
So Pr(≥3 blocks) = 1- Pr(<2 blocks)
Since Pr(≥3 blocks) more like tends to infinity and thus would be more difficult to compute as you would have to solve for the probability of 3,4 ,5,6,7........ Till infinity the more Pr(≥3 blocks) outcomes you compute, the more accurate your probability.

yeah but pretend the network rips 3 blocks in the first 3 seconds. the next 9+ minutes could kill it off.

So I would think you need poisson for

4+5+6+7+8+9+10 is pretend 1.4%

take that 6.13-1.4 = 4.73 and know you are close.

If you disregard the chance of the over block events you you be wrong.

basically because he wants exactly 3 not 4 or 5 or 6 or any higher ones.

Not doing the math for

4
5
6
7
8
9
...
20 but each one is less by a fairly large factor

Amphenomenon

sr. member

Activity: 700

Merit: 470

Hope Jeremiah 17vs7

Using this formula I got 0
Where :
Random number (K) = 3
Time interval (t)= 10
Parameter Rate(a) = 10
e = 2.71828

Silikiem

newbie

Activity: 4

Merit: 0

Sir, the probability of having exactly 3 blocks mined within the next 10 minutes is approximately 0.0613, or 6.13%.

Mia Chloe

sr. member

Activity: 448

Merit: 560

Crypto Casino and Sportsbook

Quote from: philipma1957 on March 20, 2024, 10:02:04 AM

actually this is a good question.

as the 6.13 percent answer left out all the chances above 3 blocks.

so it is close but no cigar.

I actually thought about this but I didn't make use of values ≥3 because the question asked was for exactly 3 blocks.

If not I would simply calculate that for 2 blocks and 1 block and then subtract the value from 1 to get that for the number of possible mined blocks geater than of equal to 3 since;
Pr(<2 blocks) + Pr(≥3 blocks) = 1
So Pr(≥3 blocks) = 1- Pr(<2 blocks)
Since Pr(≥3 blocks) more like tends to infinity and thus would be more difficult to compute as you would have to solve for the probability of 3,4 ,5,6,7........ Till infinity the more Pr(≥3 blocks) outcomes you compute, the more accurate your probability.

Cityhunter34

full member

Activity: 252

Merit: 57

Reward: 10M Sheen (Approx. 5000 BNB) Bounty

Quote from: Ricardo11 on March 20, 2024, 09:43:40 AM

Or 0.1%, ie 1/1000. So the probability of mining three blocks in the next 10 minutes is about 0.1% or 1/1000

I got the same thing.
To find the probability of having exactly three blocks mined, I multiplied the probability of a single block being mined three times, that is, 1/10 * 1/10 * 1/10 = 1/1000

The chance of having exactly three blocks mined in 10 minutes is 0.001

philipma1957

legendary

Activity: 4256

Merit: 8551

'The right to privacy matters'

actually this is a good question.

as the 6.13 percent answer left out all the chances above 3 blocks.

so it is close but no cigar.

if you did if for

4 blocks you would get a smaller number. say 1 percent
5 blocks you would get a smaller number than 1 percent say .1 percent

you could do that for

4,5,6,7,8,9,10 and maybe that gives a close enough estimate for more than 3 blocks maybe it is 1.4%

then take the 6.13-1.4 and get 4.73%

not perfect but if you extend to 20 blocks in 10 minutes it would be very accurate.

So I say

Poisson distribution for 3 blocks = 6.13

then add poisson for
4
5
6
7
8
9
10 subtract from poisson for 3 and very accurate

more accurate

poisson
for
11
12
13
14
15
16
17
18
19
20 add to 4-10 and subtract that from poisson for 3

since the possibility is endless but unlikely I would accept

poisson for 3 - poisson's for (4+5+6+7+8+9+10) as close enough

AmaGold70

member

Activity: 100

Merit: 35

Quote from: BlackHatCoiner on March 20, 2024, 06:14:28 AM

Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.

To calculate the probability of having exactly three blocks mined within the next 10 minutes (which is almost impossible) I used the poisson formula and I got p(3;1) =0.0613
So I'd say that there's a 6.13% chance of having exactly three blocks mined within the next 10 minutes.

I could have loved to explain how I got my answer in details but my keyboard isn't giving me every thing I need to type.

The poisson formula looks like this, p(x;a) = (e^(-a) *a^x) / x!

I used "a" to replace the symbol I couldn't find in my keyboard.

It seems newbies aren't allowed to send a picture here because I did my calculations in my notebook as it would have been easier for me to drop a picture of my calculations. I may be wrong though with my answer but am delighted to participate.

Ricardo11

full member

Activity: 532

Merit: 229

The probability of mining a new block every 10 minutes is about 1/10 or 10% on average.

If each block has a 10% chance of being mined, then the probability of mining three blocks is:

(10% * 10% * 10%) = 0.1 * 0.1 * 0.1 = 0.001

Or 0.1%, ie 1/1000. So the probability of mining three blocks in the next 10 minutes is about 0.1% or 1/1000.

Otherwise,,,

Since there is a binomial probability for each event (yes or no), the probability will be the average position of the numbers.

Given its value, the binomial probability for each event will be 1/2.

Then the probabilities for the first three events would be:

(1/2) * (1/2) * (1/2) = 1/8

BlackHatCoiner

legendary

Activity: 1512

Merit: 7340

Farewell, Leo

Quote from: rachael9385 on March 20, 2024, 06:50:15 AM

If 3 blocks was mined 10 minutes, that means each transaction would be mined within 1/10^3 and 0.0027 per transaction.
1/10^3 gotten from the λ and the 0.0027 is 1/10^3

These are some non-understandable math. Why 10^3, how did you work out 0.0027 and what does it mean?

Quote from: Ricardo11 on March 20, 2024, 06:54:10 AM

We know the formula of probability is :- possibility= (Number of favorable outcomes of events / Number of possible outcomes)

That's not the correct formula to use. Your formula makes sense in finite sets. For example, the odds of getting an even number from a dice roll.

Code:

{Total of even integers from 1 to 6} / {Total integers from 1 to 6} = 3 / 6 = 0.5

The set of all possible outcomes in the Bitcoin network within 10 minutes is infinite.

Before I unveil the answer, I want to leave the thread for a few hours. Maybe someone wants to correct the replies above.

CryptoHeadlineNews

hero member

Activity: 1092

Merit: 747

Quote from: BlackHatCoiner on March 20, 2024, 06:14:28 AM

Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.

Since Probability simply means the extent to which an event likely to occur, and we all know that it takes approximately 10 minutes for each block to be mined, I think the answer to this is what I will be giving in the calculation down below.

FORMULA FOR PROBABILITY

P(A) = Number of times A occur / Total number of possible outcomes

Where;
Number of times A occur = 10
Total number of possible outcomes = 3
Probability = ?

P(A) = (10 / 3) = 3.33

Amphenomenon

sr. member

Activity: 700

Merit: 470

Hope Jeremiah 17vs7

I wrote mine as a code in python, to be Frank my code is not professional _{i`m still working on that}

Code:

import math
Parameter = 1
RandomNumber = 3
EulerNumber = 2.71828

Probability = (Parameter ** RandomNumber ) * (EulerNumber ** (-Parameter)) / math.factorial(RandomNumber)
RoundedProbability = round(Probability, 4)
Inpercentage = str(RoundedProbability * 100)
print ('The chance of having exactly three blocks mined within the next 10 minutes = ',
RoundedProbability, 'or', Inpercentage + '%')

Poisson distribution was also spoken about on the bitcoin whitepaper in page 7 even in regards to your previous question

Etranger

hero member

Activity: 504

Merit: 816

Top Crypto Casino

Quote from: Mia Chloe on March 20, 2024, 07:05:27 AM

Quote from: Wapfika on March 20, 2024, 06:58:37 AM

I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.

But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.

Thanks for the heads up

I mistakenly substituted 3 instead of 1

I also got the same result using this formula. However, the word “exactly” in the BlackHatCoiner`s assignment confuses me. After all, this implies that exactly 3 blocks and no more should be mined in 10 minutes, and that the situation where 3 were mined and the fourth was already started to be mined is not suitable, as far as I understand. That is, after exactly ten minutes, exactly three blocks should be mined, and the extraction of the fourth should fall on the eleventh minute. And if my thoughts are correct, then Poison Distribution formula does not take this into account and the probability is calculated incorrectly, because it is greater than it actually is.

Judith87403

full member

Activity: 208

Merit: 125

Quote from: BlackHatCoiner on March 20, 2024, 06:14:28 AM

Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.

Cut-off date: 27/03/2024.

I'm using mathematics to explain the question:

probability 1/10 ...K= P(3:1) that (3 blocks per minute) = (e^-1-1^3)/3! =1/e.6 = 0.0613 ~ 6.13

^ is a power function
mean ^-1 ...-1 is to the function "e" same as ^3 to the function "1"

Alphakilo

sr. member

Activity: 450

Merit: 220

Quote from: BlackHatCoiner on March 20, 2024, 06:14:28 AM

The first question was a tribute to the whitepaper. Now let's see how good we are at math.

Question: What is the chance of having exactly three blocks mined within the next 10 minutes? You can assume that a new block is mined every 10 minutes on average.

Cut-off date: 27/03/2024.

Not like I have a choice but I preferred the first question better

These are very critical mining questions with a mix of math.
I am terrible at math.

I will return to this thread after the cut-off date - 27/03/2024 and try just study the answer of whoever gets the quiz correctly. Just maybe in the future I will be able to participate.

Aanuoluwatofunmi

sr. member

Activity: 672

Merit: 416

stead.builders

Poison Distribution explains it all

If the hashrate is not constant and we experience a memoryless event through the poison process, which describe the number of blocks that can be possily mined at a particular given time interval, Poinson distribution explains how such an event could occur on a multiple times, you can learn more from these https://careerfoundry.com/en/blog/data-analytics/what-is-poisson-distribution/

Mia Chloe

sr. member

Activity: 448

Merit: 560

Crypto Casino and Sportsbook

Quote from: Wapfika on March 20, 2024, 06:58:37 AM

I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.

But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.

Thanks for the heads up

I mistakenly substituted 3 instead of 1

Wapfika

hero member

Activity: 1288

Merit: 564

Bitcoin makes the world go 🔃

Quote from: ?? on ??

Here is my final solution
The time was same in both cases so time is constant.
0.008298

I don’t want to hijack your submission but I think you substituted wrong value to your -lambda instead of 1 you use 3 that’s why it gives you a wrong answer on this computation.

But using Poison Distribution Method will give 6.13% if you correctly substitute the value. I’m not sure if this computation will be accurate on Bitcoin mining since I don’t have enough knowledge on this area.

Topic: [Quiz] Answer the Bitcoin question and earn merits! #2 - page 2. (Read 994 times)